반응형
SMALL
사람이 생각하는 (인간의 직관)과 다른 결과를 도출하는 경우 (역설적인 상황)
임의의 N명이 모였을 때, 이 중 두명이 생일이 같을 확률은? 이란 상황을 생각해 볼 때
1년은 365일, 윤년(leap year)인 경우 2월 29일 포함하여 366일에 해당한다.
그렇다면 직관적으로 드는 느낌은 거의 없을 것이라고 기대된다.
하지만...
위키백과에 "생일문제"를 검색하면 다음과 같은 그림을 볼 수 있음
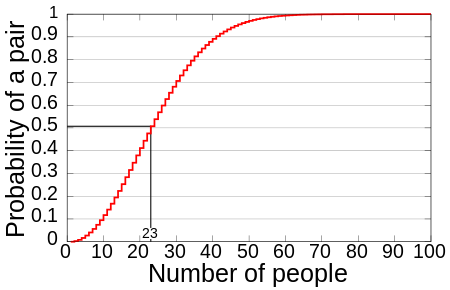
위 그림은 인간의 직관과 달리 23명 이상 모이면 이 중 두 명이 생일이 같은 확률이 1/2 (50% 이상)임을 보여준다.
N=23 , 두 명이 생일이 같을 확률: 0.51
N=50 , 두 명이 생일이 같을 확률: 0.97
n=100, 두 명이 생일이 같을 확률: 0.9999997로 거의 1에 가까움
N명의 생일이 모두 다를 확률을 여집합(complement set)으로 표기하자.
$$ P^c $$
$$ P=1- P^c $$
위 내용을 R 로 직접 작성해서 확인해 보자.
#우선 4명이라고 가정하자.
p1=365/365
p2=364/365
p3=363/365
p4=362/365
#n=1
1-p1
#n=2
1-p1*p2
#n=4
1-p1*p2*p3*p4
#그럼 이를 일반화 해보자
p=NULL
bp_func<-function(n){
for(i in 1:n){
#N명의 생일이 모두 다를 확률
p[i]=(365-i+1)/365
}
p
}
#N=23일 때, p1*p2*...*p23은 다음과 같음
bp_func(23)
prod(bp_func(23)) #0.4927028
1-prod(bp_func(23))
1-prod(bp_func(50))
1-prod(bp_func(100))
#N=1 부터 N=100까지 반복문을 이용하여 작성
Prob=NULL
for(i in 1:100){
Prob[i]<-(1-prod(bp_func(i)))
print(i)
}
df<-data.frame(N=1:100,Prob)
library(ggplot2)
ggplot(df,aes(N,Prob))+geom_point(size=3)+geom_line(size=1.1)+
geom_vline(xintercept = 23,col="red")+
geom_hline(yintercept = 0.5072972,col="red")+
theme_bw(base_size=20)

반응형
LIST
'통계학' 카테고리의 다른 글
| 생존분석: 경쟁위험(Competing risk) (0) | 2023.02.01 |
|---|---|
| 경로분석(Path analysis) (0) | 2022.03.08 |
| 분포의 중심 위치 (0) | 2022.03.08 |
| 생존분석 (0) | 2022.03.08 |
| 선형성 vs 비선형성 (Linear vs Non-linear) (0) | 2021.12.13 |